Description
Soit un réel tel que . La loi géométrique
sur 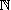 est la loi de probabilité
sur
est la loi de probabilité
sur 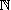 .
.
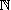 est la loi de probabilité
sur
est la loi de probabilité
sur 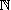 .
.
pour tout
Exemple
On dispose d'une pièce qui a une probabilité de tomber sur face et de tomber sur pile. Le nombre de lancers effectués avant d'obtenir le premier lancer dont le résultat est face définit une variable aléatoire dont la loi est la loi géométrique .Si est une variable aléatoire de loi alors est une variable aléatoire de loi .
| Espérance | Variance | Fonction génératrice |
|---|---|---|
Représentation graphique de la loi géométrique sur
de paramètre 0.65 restreint à l'intervalle .
![]()
Again
Author of the page: Sophie, Lemaire